The formula of the cost function is given by
J(mi)=1/2n*(sum of (Ypi-Yi)^2 till i reaches n)
where n is the number of data points
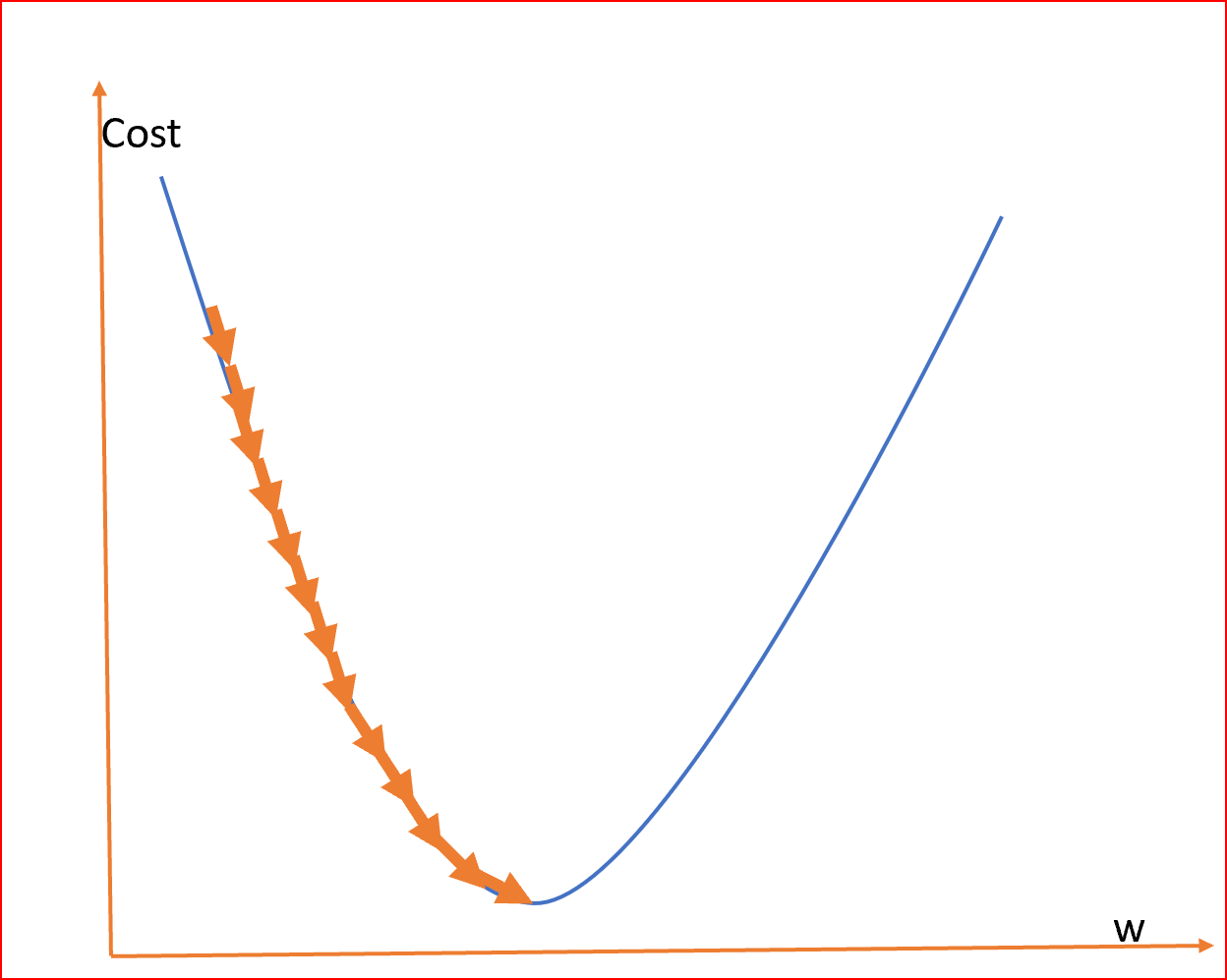
As we can see the cost function in the graph reduces till it reaches the minimum value.
This minimum value is the least error in our Linear Regression.
We need to find this minimum value
In order to find the minimum value we will use something called a Gradient Descent Algorithm or Convergence Algorithm.
So Formula for the convergence algorithm is
do{
M(new)=M(old)-(Learning Rate Alpha)*(partial derivative with respect to slope m)J(m)
Calculate cost function J(M(new)) and J(M(old))
}while(J(M(new))>J(M(old))
After the above algorithm, the least value of the cost function/Least error function is J(M(old)), and the slope for which the error is least is M(old)
Now the line will be drawn to the nearest data points with the equation
Y=M(old)Xi
where Xi is x points or an independent variable
